Description
A method to prescribe synthesized turbulent inlet
boundary conditions is given. When making LES, DES or hybrid LES-RANS a precursor
channel DNS is often used. The disadvantage of this method is that it is difficult
to re-scale the DNS fluctuations to higher Reynolds numbers.
The
synthesized isotropic turbulent fluctuations are generated at the inlet plane
with a prescribed turbulent length scale and energy spectrum. A large number of
independent realizations are generated. When running the unsteady CFD code a correlation in time between these
realization is introduced via an asymmetric, non-truncated time filter.
In this way the turbulent time scale of the synthesized isotropic turbulent fluctuations is prescribed.
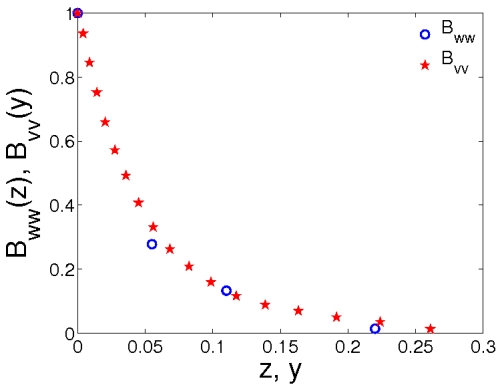
Isotropic fluctuations are generated above. However, turbulence is generally anisotropic,
The method can be summarized by the following steps.
-
A Reynolds stress tensor, ⟨v'i v'j ⟩
is taken from DNS data for turbulent channel flow.
- The principal directions (the eigenvectors),
are computed for the ⟨v'i v'j ⟩ tensor.
The eigenvalues are normalized so that their sum
is equal to three.
This ensures that the kinetic energy of the synthetic fluctuations does not
change during transformation.
- Isotropic synthetic fluctuations are then generated in the principal
directions.
- The isotropic synthetic fluctuations in the principal directions
are multiplied by the square-root of the normalized eigenvalues.
This gives a new field of fluctuations.
- The new fluctuations
are transformed to the computational coordinate system; the transformation matrix
consists of the three eigenvectors.
- The Python and Matlab/Octave codes for
generating the anisotropic fluctuations can be downloaded below.
Downloads
Here Python and Matlab/Octave Matlab files can be downloaded to generate isotropic and anisotropic
synthetic fluctuations described above. The
method is described in detail in the PDF files (see References below).
Movie
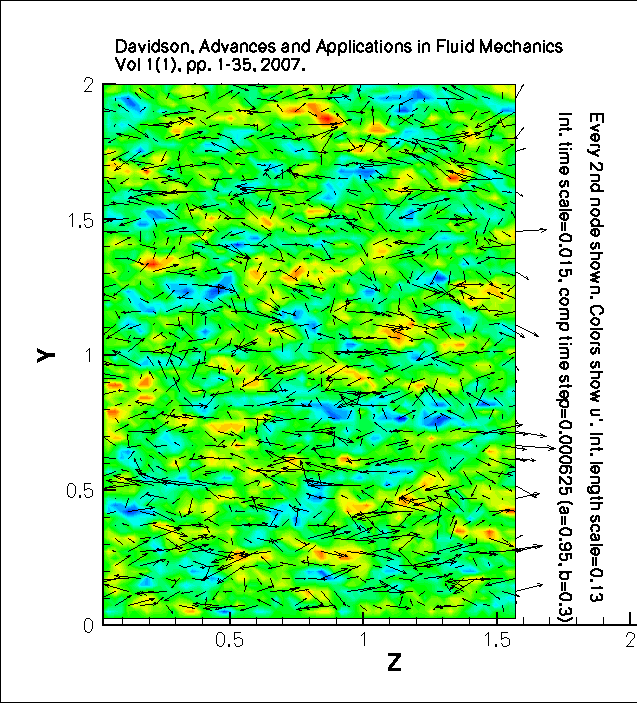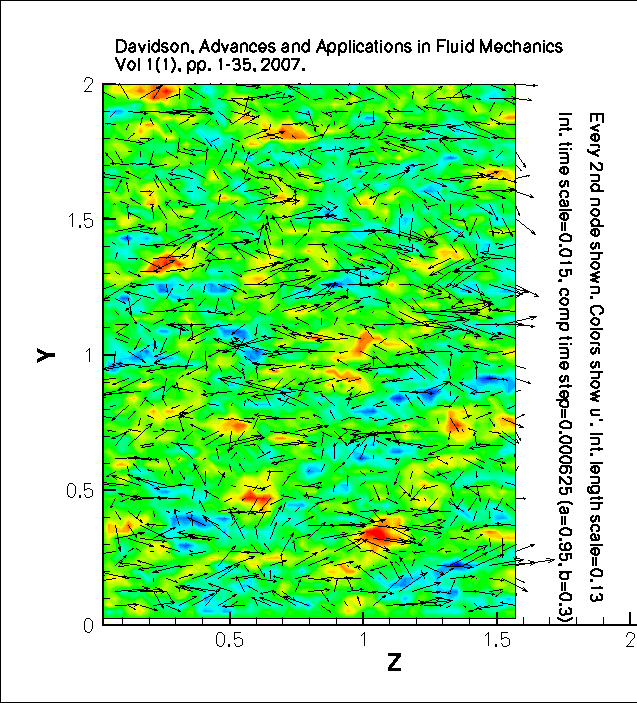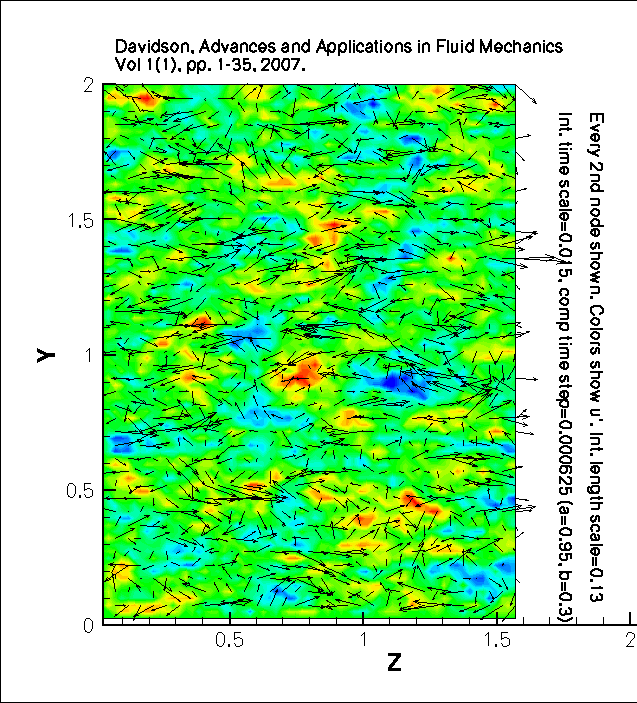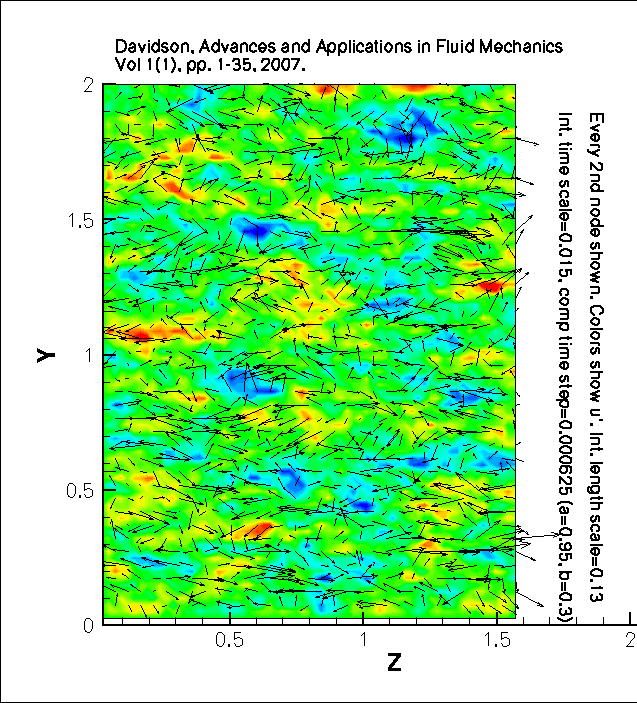
Movies which show
isotropic synthetic inlet fluctuations.
Integral time scale=0.015, computational time step=0.000625 (a=0.95, b=0.3)
Integral length scale=0.13
Colors show u'.
movie (7.4MB)
Integral time scale=0.015, computational time step=0.000625 (a=0.95, b=0.3)
Integral length scale=0.40
Colors show u'.

movie (6.2MB)

REFERENCES
-
BILLSON, M
"Computational Techniques for Turbulence Generated Noise",
PhD thesis, Dept. of Thermo and Fluid Dynamics, Chalmers
University of Technology, Göteborg, 2004.
View PDF file
Errata: View PDF file
-
M. Billson, L.-E. Eriksson and L. Davidson
Jet Noise Modeling Using Synthetic Anisotropic Turbulence",
10th AIAA/CEAS Aeroacoustics Conference, AIAA 2004-3028, Manchester, United Kindom, 2004.
View PDF
file
-
L. Davidson
"Using Isotropic Synthetic Fluctuations as Inlet Boundary Conditions for Unsteady Simulations"
Advances and Applications in Fluid Mechanics, Vol. 1(1), pp. 1-35, 2007.
View PDF file
-
L. Davidson
"HYBRID LES-RANS: Inlet Boundary Conditions for Flows Including Recirculation",
5th International Symposium on
Turbulence and Shear Flow Phenomena, Vol. 2, pp. 689-694, 27-29 August, Munich, Germany, 2007.
View PDF file
-
Appendix: "Computation of wavenumber vector and angles"
View PDF file
-
L. Davidson
"Inlet fluctuating boundary conditions for 3D Hill Flow"
View PDF file
-
L. Davidson and S.-H. Peng
"Embedded LES Using PANS",
I6th AIAA Theoretical Fluid Mechanics Conference, AIAA paper 2011-3108
27 - 30 Jun 2011, Honolulu, Hawaii.
View PDF file
-
L. Davidson
"Large Eddy Simulation of Heat Transfer in Boundary Layer and Backstep Flow Using PANS",
Turbulence, Heat and Mass Transfer 7
Hanjalic, Y. Nagano, D. Borello and S. Jakirlic (Editors),
Begell House, Inc., 2012
View PDF file
-
L. Davidson and S.-H. Peng
"Embedded Large-Eddy Simulation Using the Partially
Averaged Navier-Stokes Model", AIAA J,
Vol. 51(5), pp. 1066-1079, 2013.
DOI
-
L. Davidson
Fluid mechanics, turbulent flow and turbulence modeling, course material in MSc courses,
Division of Fluid Dynamics, Dept. of Applied Mechanics, Chalmers University of Technology,
Göteborg, 2010
View PDF file
|